Complete Homeschool Math Curriculum Using Manipulatives (K-6)

If you’ve watched your child build elaborate structures with blocks or sort buttons by color with intense concentration, you’ve already seen mathematical thinking in action. What looks like play is actually your child’s brain doing exactly what it needs to do: understanding abstract concepts through concrete experience.

This is why manipulative-based math works so powerfully for homeschoolers. And this is why you don’t need expensive boxed curricula to give your children a rigorous, complete math education from kindergarten through sixth grade.

What you need instead is understanding of how children develop mathematical thinking, a collection of hands-on materials (many you already own), and a framework that guides you through each developmental stage. That’s what this guide provides.

Why Manipulatives Aren’t Optional for Young Mathematicians

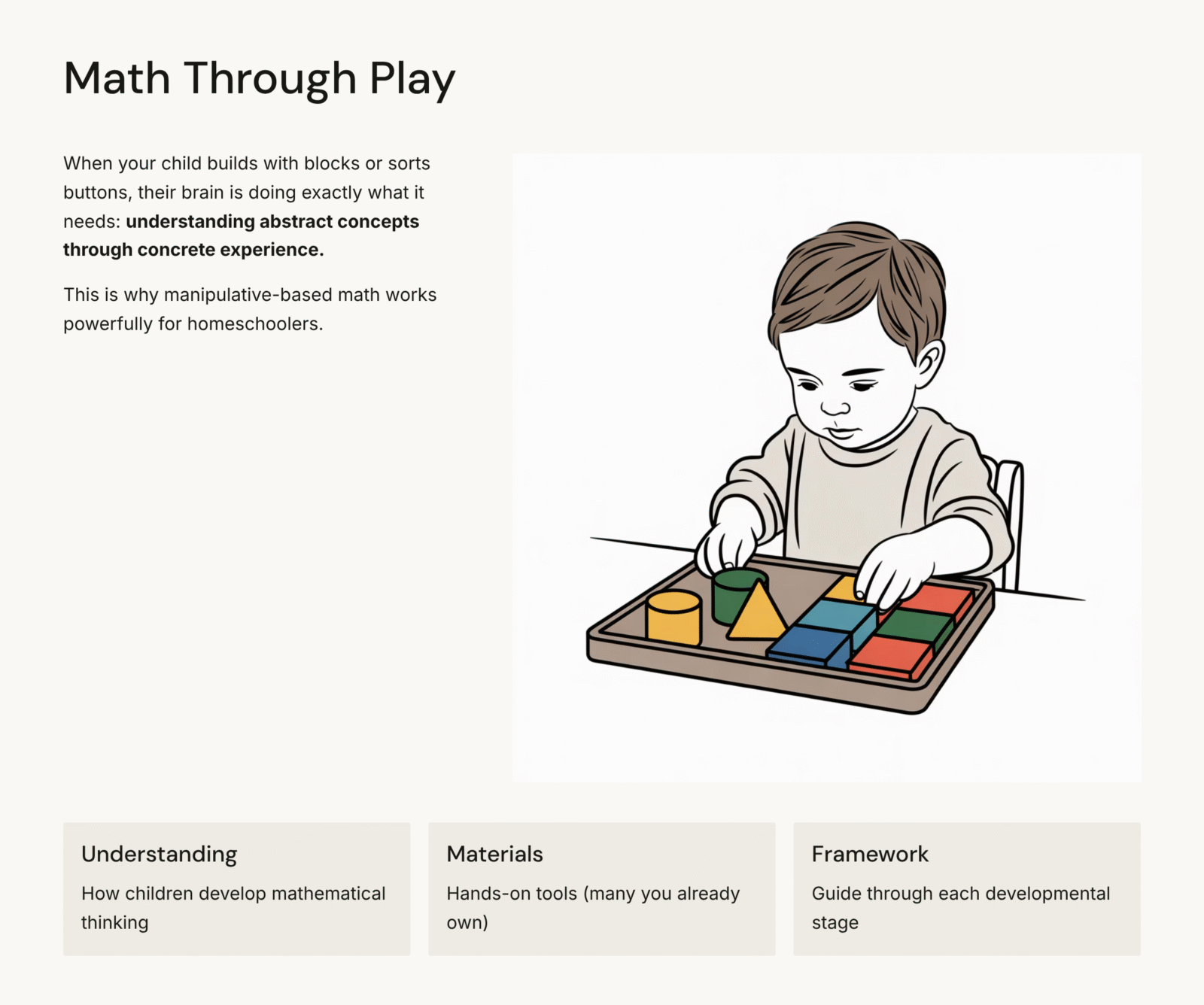
Here’s what educational pioneers from Froebel to Montessori to modern neuroscience all agree on: children under 12 learn mathematical concepts through physical experience first, symbolic representation second.

When your 6-year-old moves 3 blocks and adds 4 more, she’s not just illustrating 3+4=7. She’s building the neural pathways that will eventually allow her to understand algebra. When your 9-year-old uses fraction tiles to discover that 1/2 equals 2/4, he’s experiencing mathematical truth rather than memorizing a rule he’ll forget by next Tuesday.

The progression works like this:

Concrete stage (roughly ages 5-8): Children need to touch, move, and manipulate physical objects to understand quantity, operations, and relationships. This isn’t remedial—this is foundational.

Representational stage (roughly ages 8-10): Children can work with pictures and diagrams that represent mathematical concepts. They’re building the bridge from physical to abstract.

Abstract stage (roughly ages 10+): Children can work with numbers and symbols alone. But even here, returning to manipulatives for new concepts accelerates understanding.

What does this mean practically? A child who masters multiplication with manipulatives at age 8 will find multi-digit division simpler at age 10. A child who explores fractions with pattern blocks won’t stumble when decimals appear. You’re not slowing them down—you’re building unshakeable foundations.

The Core Principles That Make This Curriculum Work

Before we dive into grade-by-grade specifics, you need to understand the three principles that hold this entire approach together.

1. Progress Through Mastery, Not Age

Your curriculum should adapt to your child, not the other way around. If your 7-year-old needs more time with single-digit addition, give it. If your 5-year-old is ready for skip counting patterns, don’t hold back.

Watch for these mastery indicators:

• Your child can explain the concept to someone else
• They can solve problems without the manipulatives (but still prefer them for complex problems)
• They notice the concept appearing in daily life
• They make connections between related ideas

2. Spiral Learning Over Linear Progression

You’ll revisit the same mathematical concepts multiple times with increasing complexity. Your kindergartener sorts objects. Your second grader creates patterns. Your fifth grader uses those same sorting and patterning skills for data analysis and algebraic thinking.

This isn’t repetition—it’s deepening. Each time your child encounters a concept, they bring more experience and make new connections.

3. Integration Over Isolation

Real mathematical thinking doesn’t happen in 20-minute workbook sessions. It happens when your child measures ingredients for cookies, calculates how many weeks until their birthday, or figures out if their allowance covers that toy they want.

Your manipulative work provides the foundation. Daily life provides the application. Together, they create mathematical fluency.

Your Complete K-6 Curriculum Framework

Here’s your year-by-year guide with specific activities, materials, and observable outcomes. Each grade level builds systematically on the previous year while introducing new concepts at the concrete level.

Kindergarten (Ages 5-6): Building Number Sense

Core Concepts:

• Counting to 20 (and beyond with interest)
• One-to-one correspondence
• More/less relationships
• Simple patterns
• Basic shapes and spatial relationships

Essential Activities:

Number Recognition and Counting (15 minutes daily)

Start with physical objects your child can count and move. Use wooden blocks, buttons, dried beans, or dedicated counting materials like colored rings or cubes.

Have your child:

• Count out specific quantities (give me 7 blocks)
• Match numeral cards to quantities (put 5 buttons on the card that says “5”)
• Compare sets (which pile has more?)
• Create sets to match a numeral

Observable success: Your child counts accurately to 10 by touching each object once, can look at a set of 5 objects and recognize “five” without counting, and can create a set of any quantity 1-10 when asked.

Pattern Work (10 minutes, 3x weekly)

Patterns are the heart of mathematical thinking. Begin with simple AB patterns (red-blue-red-blue) and extend to ABC and ABB patterns.

Use whatever you have:

• Colored blocks or beads
• Pattern blocks (hexagons, triangles, squares, trapezoids, rhombuses, triangles)
• Buttons sorted by color or size
• Natural materials like pinecones and acorns
• Spielgaben gifts 7-10 (but honestly, Lego works just as well)

Have your child:

• Copy patterns you create
• Extend patterns (what comes next?)
• Find the mistake in patterns you make with one error
• Create their own patterns and describe the rule

Observable success: Your child can create an ABC pattern independently and explain the pattern rule in their own words (“It goes big, small, medium, big, small, medium”).

Shape Exploration (10 minutes, 2x weekly)

Don’t just name shapes—let your child discover their properties through play and building.

Provide:

• Basic wooden blocks (cubes, cylinders, rectangular prisms, triangular prisms)
• Pattern blocks
• Tangram pieces
• Drawing materials to trace and create shapes

Activities:

• Build structures and name the shapes used
• Sort shapes by attributes (has corners, doesn’t have corners)
• Trace shapes and count sides and corners
• Find shapes in the environment during daily walks

Observable success: Your child can identify circle, square, triangle, rectangle by name, can describe them by attributes (“a square has four equal sides”), and spots shapes in the real world without prompting.

Materials Investment: $30-60 if starting from nothing (wooden blocks, pattern blocks, and counting objects)

Time Commitment: 30-40 minutes daily

First Grade (Ages 6-7): Operations Foundation

Core Concepts:

• Addition and subtraction within 20
• Place value (tens and ones)
• Measurement basics
• Money concepts (counting coins)
• Time (hour and half-hour)

Essential Activities:

Addition and Subtraction (20 minutes daily)

Now you’re building the understanding that addition combines quantities and subtraction separates them. Use the same manipulatives from kindergarten, but with more intentional mathematical thinking.

The progression:

1. Acting out stories: “You have 5 toy cars. Grandma gives you 3 more. How many now?” Let your child physically gather 5 objects, add 3 more, and count the total.
2. Part-part-whole relationships: Use two colors of counters. Show 8 counters total—5 red and 3 blue. Have your child see that 5+3=8, but also 3+5=8. Hide one color and ask “If 8 total and 5 are red, how many are blue?”
3. Number bonds: Use manipulatives to discover all the ways to make numbers 5-10. Make this a game: “How many different ways can we make 7?”
4. Missing addend problems: “I have 6 counters here. I need 10 total. How many more do I need?” This is the foundation for subtraction understanding.

Observable success: Your child can solve addition and subtraction problems within 10 using manipulatives efficiently (not counting by ones), can explain their thinking, and is beginning to solve simple problems mentally without needing physical objects.

Place Value Foundation (15 minutes, 4x weekly)

This is where many math curricula fail children. They rush to symbolic representation before children understand what “24” actually means.

Use base-ten blocks (units, rods, and flats) or make your own with:

• Dried beans for ones
• Popsicle sticks bundled in tens with rubber bands
• Graph paper where your child colors ten squares and calls it “one ten”

Activities:

• Count objects and group them in tens
• Build two-digit numbers with blocks (make 34 with 3 ten-rods and 4 unit cubes)
• Compare numbers using blocks (is 28 more than 31?)
• Add and subtract using place value (24+10 means adding one more ten-rod)

Observable success: Your child can represent any number 1-100 with manipulatives, can explain why 24 is “2 tens and 4 ones,” and understands that 24+10=34 because you’re adding one more group of ten.

Measurement Exploration (15 minutes, 2x weekly)

Measurement makes math tangible and purposeful. Your child should measure everything in sight.

Provide:

• Rulers (both standard and metric if possible)
• Measuring cups and spoons
• Non-standard units (paper clips, Lego bricks, shoes)
• Balance scales for weight comparison
• Analog clock for time

Activities:

• Measure toys, furniture, plants using non-standard units first
• Progress to measuring in inches and centimeters
• Compare measurements (Which is longer? By how much?)
• Estimate before measuring
• Involve your child in cooking (measuring ingredients)
• Practice telling time during daily routines

Observable success: Your child can measure objects to the nearest inch or centimeter, can estimate reasonably, and is beginning to understand what different units mean in real contexts.

Materials Investment: $40-70 (base-ten blocks, ruler, measuring cups, analog clock)

Time Commitment: 45-60 minutes daily

Second Grade (Ages 7-8): Computational Fluency

Core Concepts:

• Addition and subtraction within 100
• Multiplication introduction (repeated addition and skip counting)
• Place value through hundreds
• Fractions (halves, thirds, fourths)
• Measurement with standard units

Essential Activities:

Multi-Digit Addition and Subtraction (20 minutes daily)

Continue using base-ten blocks for every problem until your child can explain the process clearly. Don’t rush to algorithms.

The progression:

1. Without regrouping: 34+12 using 3 tens and 4 ones, plus 1 ten and 2 ones
2. With regrouping: 28+15 where your child discovers they need to trade 10 ones for another ten-rod
3. Subtraction without regrouping: 45-23
4. Subtraction with regrouping: 42-17 where they need to “break apart” a ten-rod into 10 ones

Have your child:

• Build both numbers with blocks
• Combine or separate the quantities
• Trade (regroup) when necessary
• Record what they did symbolically only after they understand physically

Observable success: Your child can solve two-digit addition and subtraction problems with regrouping using manipulatives, can explain why regrouping works, and is beginning to solve simpler problems (no regrouping) mentally.

Multiplication as Groups (15 minutes, 4x weekly)

Don’t introduce multiplication as memorization. Introduce it as a convenient way to count equal groups.

Use any objects that can be grouped:

• Counters arranged in arrays (rows and columns)
• Egg cartons showing “groups of 12”
• Muffin tins showing “4 groups of 6”
• Number lines for skip counting
• Pattern blocks or colored tiles for area models

Activities:

• Create equal groups (make 5 groups with 3 in each)
• Skip count with physical jumps on a number line (2, 4, 6, 8…)
• Build arrays with tiles (3 rows of 4 is the same as 4 rows of 3)
• Solve real problems (If each friend gets 4 cookies and we have 5 friends, how many cookies total?)

Focus on 2s, 5s, and 10s this year. Let your child discover the patterns rather than memorizing facts.

Observable success: Your child can show 3×4 with manipulatives in multiple ways (groups, arrays, skip counting), can explain that 3×4 means “3 groups of 4” or “4+4+4,” and is beginning to recall 2s, 5s, and 10s without counting.

Fraction Introduction (15 minutes, 3x weekly)

Fractions terrify many children because they’re introduced symbolically. Avoid that trap.

Essential materials:

• Fraction circles or bars (these are worth buying—$15-25 set)
• Paper for folding
• Play dough for cutting
• Pattern blocks (hexagons = 1 whole, trapezoids = 1/2, triangles = 1/6)
• Food (actual pizza, sandwiches cut into pieces, brownies)

Activities:

• Fold paper into halves, fourths, eighths and color one part
• Use fraction circles to show that 1/2 is bigger than 1/4 (even though 4 is bigger than 2)
• Find equivalent fractions with pattern blocks (1/2 hexagon = 3/6 hexagon)
• Share food fairly (cut this brownie so 4 people get equal pieces)

The goal isn’t notation yet—it’s understanding that fractions represent parts of a whole, and the denominator tells you how many equal parts.

Observable success: Your child can divide objects or shapes into equal parts, can explain why 1/2 is larger than 1/4, and is beginning to recognize equivalent fractions through physical comparison.

Materials Investment: $30-50 (fraction circles/bars, additional manipulatives)

Time Commitment: 50-60 minutes daily

Third Grade (Ages 8-9): Mathematical Relationships

Core Concepts:

• Multiplication and division mastery
• Fractions (comparing, equivalent fractions, simple addition)
• Multi-digit addition and subtraction
• Area and perimeter
• Time and money application

Essential Activities:

Multiplication and Division Connection (25 minutes daily)

This is the year multiplication facts should become fluent—but through understanding, not flashcards alone.

Continue using manipulatives for all new concepts:

• Arrays with tiles or graph paper
• Area models with base-ten blocks
• Skip counting on number lines
• Equal groups with counters

The critical insight: Division is the inverse of multiplication. When your child builds 4×6=24 with an array, they’re simultaneously seeing 24÷4=6 and 24÷6=4.

Have your child:

• Build each multiplication fact with arrays (Yes, even 9×8. Especially 9×8.)
• Write the related division facts for every multiplication fact
• Solve word problems where they choose multiplication or division
• Discover patterns (all multiples of 5 end in 0 or 5)

Use the “known facts strategy”: If your child knows 5×6=30, they can figure out 6×6 by adding one more group of 6.

Observable success: Your child can demonstrate any multiplication fact through 10×10 with manipulatives, can explain why 6×7 equals 7×6, knows most facts fluently, and can use known facts to derive unknown facts.

Fraction Operations (20 minutes, 4x weekly)

Now you’re building on last year’s foundation to compare fractions and add fractions with like denominators.

Continue using fraction circles, bars, and pattern blocks. Add:

• Number lines with fractions marked
• Paper folding to create equivalent fractions
• Food for real-world fraction work

Activities:

• Compare fractions with the same denominator (3/8 vs 5/8)
• Compare fractions with different denominators using manipulatives
• Find equivalent fractions (fold 1/2 into fourths to show 1/2 = 2/4)
• Add fractions with same denominator (2/8 + 3/8 using fraction circles)
• Solve problems (ate 1/4 of pizza, friend ate 2/4, how much total?)

Don’t rush to common denominators. Let your child see why 1/2 + 1/4 requires thinking about equal-sized pieces first.

Observable success: Your child can compare any two fractions using manipulatives, can find equivalent fractions, and can add fractions with like denominators while explaining their reasoning.

Area and Perimeter (15 minutes, 3x weekly)

This topic comes alive with hands-on exploration, not formulas.

Provide:

• Square tiles or graph paper
• Rulers
• String or yarn
• Base-ten blocks (use unit cubes to fill in rectangles)

Activities:

• Build rectangles with tiles and count how many cover the space (area)
• Walk around the rectangle counting the tiles on the edges (perimeter)
• Discover that different shapes can have the same area but different perimeters
• Measure rooms in your house
• Design a garden plot with specific area constraints

Let your child discover that area is about covering space (measured in square units) and perimeter is about distance around (measured in linear units).

Observable success: Your child can measure or calculate area by counting square units, can measure perimeter accurately, and understands these represent different attributes of shapes.

Materials Investment: $20-40 (graph paper, additional tiles if needed)

Time Commitment: 60 minutes daily

Fourth Grade (Ages 9-10): Bridge to Abstract Thinking

Core Concepts:

• Multi-digit multiplication and division
• Decimals introduction
• Fraction operations (addition, subtraction, multiplication)
• Angles and geometric measurement
• Data analysis with graphs

Essential Activities:

Multi-Digit Multiplication (25 minutes daily)

Don’t jump to the standard algorithm yet. Build understanding with area models first.

Use:

• Base-ten blocks (rods and flats for place value)
• Graph paper for area models
• Arrays with smaller manipulatives

The area model progression for 24×13:

1. Build a rectangle that’s 24 units by 13 units using graph paper
2. Break it into sections: (20×10) + (20×3) + (4×10) + (4×3)
3. Calculate each section
4. Add the partial products

This is how multiplication actually works. The standard algorithm is just a shorthand for this process.

Have your child:

• Solve every multi-digit problem with area models first
• Break problems into partial products
• Estimate before calculating (24×13 is about 25×10=250)
• Solve real-world problems (If each box holds 24 pencils and we need 13 boxes, how many pencils total?)

Observable success: Your child can solve 2-digit by 2-digit multiplication using area models, can explain why you break numbers apart by place value, and is beginning to use the standard algorithm as a shorthand for their understanding.

Decimals as Fractions (20 minutes, 4x weekly)

Decimals confuse children when they’re presented as a separate topic from fractions. They’re not separate—they’re fractions written in a different notation.

Use:

• Base-ten blocks (flat=1, rod=0.1, unit=0.01)
• Decimal grids (10×10 squares)
• Money (perfect decimal manipulative)
• Metersticks marked in centimeters

Activities:

• Represent decimals with base-ten blocks (2.34 is 2 flats, 3 rods, 4 units)
• Show the connection: 0.7 = 7/10, 0.25 = 25/100 = 1/4
• Add decimals using blocks (2.4 + 1.3)
• Compare decimals (which is more: 0.3 or 0.29?)
• Use money for real calculations

Don’t teach “line up the decimal points” as a rule. Let your child discover why place value alignment matters through manipulatives.

Observable success: Your child can represent any decimal through hundredths with manipulatives, understands decimals as fractions, can add and subtract decimals, and is beginning to work symbolically.

Advanced Fraction Work (20 minutes, 3x weekly)

Continue with fraction circles and bars, but add complexity.

Focus on:

• Adding and subtracting fractions with unlike denominators
• Multiplying fractions (using area models or paper folding)
• Finding fractions of whole numbers (1/3 of 12)
• Word problems requiring fraction thinking

For addition with unlike denominators, your child should use manipulatives to discover why they need common denominators: you can’t add 1/3 and 1/4 directly because the pieces are different sizes.

Observable success: Your child can add fractions with unlike denominators using manipulatives to find equivalent fractions, can find a fraction of a whole number, and can explain why procedures work.

Materials Investment: $15-30 (decimal grids, additional graph paper)

Time Commitment: 60-75 minutes daily

Fifth Grade (Ages 10-11): Abstract Thinking Emerges

Core Concepts:

• All operations with decimals
• Fraction division
• Volume and 3D measurement
• Ratios and proportions
• Introduction to negative numbers
• Algebraic thinking (variables and expressions)

Essential Activities:

Decimal Operations (20 minutes daily)

Your child should be comfortable with most decimal work symbolically now, but use manipulatives for multiplication and division.

For decimal multiplication (like 2.4 × 3.5):

• Use area models on decimal grids
• Show how 2.4 × 3.5 relates to 24 × 35 (just shift the decimal point)

For decimal division:

• Use base-ten blocks for simple problems
• Connect to fraction division (dividing by 0.5 is the same as dividing by 1/2)

Have your child:

• Estimate decimal operations before calculating
• Solve multi-step problems
• Work with money scenarios (compound interest, sales tax, discounts)

Observable success: Your child can perform all operations with decimals accurately, can explain why procedures work, and can estimate to check reasonableness.

Volume and 3D Thinking (20 minutes, 4x weekly)

Volume is area thinking extended into three dimensions.

Essential materials:

• Unit cubes (wooden 1cm cubes are ideal—buy 200)
• Boxes of various sizes
• Base-ten blocks
• Measuring cups and containers

Activities:

• Fill boxes with unit cubes to find volume
• Build rectangular prisms with specific volumes
• Discover the volume formula through repeated building (V = l × w × h)
• Measure liquid volume with graduated cylinders
• Compare volume and capacity

Let your child discover that a 2×3×4 prism needs 24 unit cubes to fill it completely. That’s what volume means.

Observable success: Your child can calculate volume by counting unit cubes or using the formula, can visualize 3D shapes, and understands volume as three-dimensional space.

Ratios and Proportions (20 minutes, 3x weekly)

Ratios emerge naturally from all your previous fraction work.

Use:

• Colored counters for ratio relationships
• Recipes for doubling/halving (practical proportions)
• Scale drawings and maps
• Pattern blocks for ratio tables

Activities:

• Create equivalent ratios with manipulatives (2:3 is the same as 4:6)
• Solve proportion problems (if 2 cups flour makes 12 cookies, how much flour for 30 cookies?)
• Work with scale (if 1 inch = 5 feet on this map…)
• Mix paint colors in specific ratios

Observable success: Your child can recognize and create equivalent ratios, can solve proportion problems using manipulatives or diagrams, and can explain ratio relationships.

Introduction to Negative Numbers (15 minutes, 2x weekly)

Negative numbers need concrete models.

Use:

• Two-colored counters (red=negative, yellow=positive)
• Number lines (especially vertical ones showing elevation/temperature)
• Integer chips
• Real contexts (temperature, money owed, elevation)

Activities:

• Show addition and subtraction on number lines
• Use colored counters for operations (adding a negative is like adding red chips)
• Solve real problems (temperature drops, money owed)
• Create zero pairs (1 + -1 = 0)

Observable success: Your child can add and subtract integers using manipulatives or number lines, understands negative numbers as opposites, and can explain operations conceptually.

Materials Investment: $40-60 (unit cubes, integer manipulatives)

Time Commitment: 75 minutes daily

Sixth Grade (Ages 11-12): Formal Mathematical Thinking

Core Concepts:

• All fraction, decimal, and integer operations
• Expressions and equations (algebra foundation)
• Percent
• Statistics and probability
• Advanced geometry (area of triangles, circles)

Essential Activities:

Pre-Algebra Foundation (25 minutes daily)

Your manipulative work culminates in algebraic thinking, but you still use hands-on tools for new concepts.

Use:

• Algebra tiles (worth investing in—$20-30)
• Balance scales (for equation solving)
• Pattern blocks for visual patterns that become algebraic expressions

Activities:

• Represent expressions with algebra tiles (2x + 3)
• Solve simple equations using balance scales (if 2x + 3 = 11, what’s x?)
• Create tables from patterns and write expressions
• Graph simple relationships

The goal isn’t symbolic manipulation yet—it’s understanding variables as placeholders and equations as balanced relationships.

Observable success: Your child can represent simple expressions with manipulatives, can solve one-step equations using concrete models, and is beginning to work symbolically with understanding.

Percent as Another Fraction Representation (20 minutes, 4x weekly)

Percent is just another way to write fractions and decimals. Don’t treat it as separate.

Use:

• 10×10 grids (perfect for percent)
• Base-ten blocks
• Real situations (sales, tips, discounts, interest)

Have your child:

• Shade 10×10 grids to show percents
• Connect percents to fractions and decimals (25% = 1/4 = 0.25)
• Calculate percents using grids first, then mentally
• Solve real problems

Observable success: Your child understands percent as “per hundred,” can convert between fractions, decimals, and percents, and can calculate percents in practical situations.

Probability and Statistics (15 minutes, 3x weekly)

Make this experimental, not theoretical.

Materials:

• Dice, spinners, coins
• Colored cubes in bags
• Cards
• Graph paper for data collection

Activities:

• Conduct experiments (flip coin 50 times, record results)
• Calculate experimental probability
• Compare to theoretical probability
• Create graphs of collected data
• Calculate mean, median, mode with actual datasets

Let your child discover that probability describes likelihood, not certainty, through repeated experiments.

Observable success: Your child can conduct probability experiments, can calculate basic probabilities, can create appropriate graphs for data, and can calculate measures of center.

Materials Investment: $30-50 (algebra tiles, additional materials)

Time Commitment: 60-75 minutes daily

Essential Materials List by Grade Level

Kindergarten-1st Grade Foundation:

• Wooden blocks or colored cubes (100 pieces minimum) — $20
• Pattern blocks set — $15
• Counting objects (buttons, beans, or wooden counters) — $5
• Basic ruler — $2

2nd-3rd Grade Addition:

• Base-ten blocks (units, rods, flats) — $25
• Fraction circles or bars — $20
• Analog clock (learning clock) — $8
• Measuring cups and ruler — $10

4th-5th Grade Addition:

• Unit cubes for volume (200 pieces) — $30
• Decimal grids (printable or purchased) — $10
• Integer chips or two-colored counters — $15
• Graph paper (buy in bulk) — $5

6th Grade Addition:

• Algebra tiles — $25
• 10×10 percent grids — $8
• Probability materials (dice, spinners) — $10

Total Investment for K-6: Approximately $200-250 over seven years

Alternative approach: Spielgaben complete set ($300-400) includes blocks, pattern materials, manipulatives, and structured activities covering most of these needs, plus extensions through high school. But you can absolutely create a complete program with individual purchases or homemade alternatives.

Implementation Strategy: Making This Work in Your Homeschool

Start Where Your Child Is, Not Where They “Should” Be

Your 7-year-old might still need manipulatives for addition within 10. Your 6-year-old might be ready for multiplication concepts. Both are normal.

Assess understanding, not age. Can your child explain the concept? Can they solve problems without manipulatives? Can they apply the concept to new situations? If yes to all three, move forward. If no to any, spend more time at the current level.

Schedule for Success

Minimum effective dose: 30-40 minutes daily for K-1, 45-60 minutes for 2nd-4th, 60-75 minutes for 5th-6th.

Optimal structure:

• Core concept work (new material): 20-30 minutes
• Practice with manipulatives (review): 15-20 minutes
• Applied problem-solving: 10-15 minutes
• Mental math/games: 5-10 minutes

You don’t need 90-minute math marathons. You need focused, hands-on work daily.

What Success Looks Like at Each Stage

Early elementary (K-2): Your child solves problems enthusiastically with manipulatives, can explain their thinking, and is beginning to visualize operations mentally. They may still count on fingers occasionally—that’s fine.

Middle elementary (3-4): Your child reaches for manipulatives for new or challenging problems but can solve familiar problems mentally. They explain their reasoning using mathematical language and make connections between concepts.

Upper elementary (5-6): Your child uses manipulatives primarily for new concepts, can work symbolically with understanding, and chooses efficient strategies for different problem types. They think mathematically about situations in daily life.

When to Transition to Symbolic Work

Never make the transition abruptly. Instead, work in parallel: manipulatives alongside written work.

The progression:

1. Child solves with manipulatives while you record symbolically
2. Child solves with manipulatives and records afterward
3. Child decides whether to use manipulatives or work symbolically
4. Child works symbolically but can demonstrate with manipulatives if asked

Even after transitioning to symbolic work, return to manipulatives when:

• Introducing new concepts
• Your child seems confused
• Problems become more complex
• Your child requests them

Adapting for Multiple Children

Teaching multiple grades simultaneously? You’re actually in an ideal situation.

Share manipulative time: Younger children watch older children work with more complex concepts. Older children reinforce understanding by explaining to younger siblings.

Differentiate the problem, not the manipulative: All ages can use base-ten blocks. Your first grader adds 2-digit numbers. Your fourth grader multiplies them. Your sixth grader uses them to represent algebraic expressions.

Create mixed-age challenges: “Everyone use pattern blocks to create a design. Kindergartener, tell me the shapes you used. Second grader, find the area. Fourth grader, what fraction of the total is each color?”

Troubleshooting Common Challenges

“My child resists manipulatives—they want to do ‘real math’ like worksheets.”

They’ve internalized the message that manipulatives are for struggling students. Reframe: “Mathematicians use models to solve complex problems. We’re going to solve this problem three ways—with blocks, with a diagram, and with numbers—and see which method is most efficient.”

“This is taking so long. We’re moving much slower than the curriculum guide suggests.”

Good. You’re building understanding, not checking boxes. A child who truly masters single-digit addition with manipulatives will fly through multi-digit problems later. Slow down now to speed up later.

“My child can solve problems with manipulatives but struggles with symbolic work.”

They’re in the normal progression from concrete to abstract. Keep the parallel practice going: manipulatives for challenging problems, symbolic work for easier problems. The bridge will build naturally.

“We don’t have room to store all these manipulatives.”

You need less than you think. One large plastic container holds: base-ten blocks, pattern blocks, fraction circles, counting objects, and dice. A second container for building blocks. Store in a closet, under a bed, or on a shelf. This isn’t elaborate—it’s essential.

Beyond the Manipulatives: Real-World Math Application

The manipulative work isn’t the endpoint—it’s the foundation for seeing mathematics everywhere.

In the kitchen: Measuring, fractions, ratios, time, temperature, unit conversion

In the store: Money, percentages (discounts), unit pricing, estimation, budgeting

On trips: Distance, time, speed, map reading, scale, data collection

In hobbies: Sports statistics, craft measurements, music ratios, building projects, garden planning

Your goal is a child who thinks: “That’s a math problem—I can solve it.”

Your Next Steps

You have the framework. You have the grade-by-grade guide. You understand the philosophy.

Now you need the daily implementation system.

I’ve created a complete downloadable curriculum guide that gives you:

• Week-by-week lesson plans for each grade level
• Printable manipulative templates for materials you can make
• Problem sets designed for hands-on exploration
• Progress checklists to track mastery, not just completion
• Adaptations for learning differences and multiple children

[Download your complete K-6 manipulative math curriculum guide here]

This isn’t another rigid curriculum to follow blindly. It’s a flexible framework that adapts to your child’s pace, your family’s rhythm, and your educational philosophy—whether that’s Montessori, Waldorf, Charlotte Mason, or your own unique blend.

Your children can develop deep mathematical understanding without expensive programs, without stress, and without shortcuts that create gaps later. They can build the kind of foundation that makes higher math feel intuitive rather than mysterious.

Start with the manipulatives you have. Start where your child is. Start tomorrow.

And watch what happens when children build mathematics with their hands before they write it with their pencils.